jueves, 30 de julio de 2015
Alegría: Gracias GOOGLE
Alegría: Gracias GOOGLE: Gracias GOOGLE por felicitarme en el día de mi cumpleaños. Gracias, Gracias, Gracias.....
jueves, 23 de julio de 2015
martes, 21 de julio de 2015
sábado, 18 de julio de 2015
viernes, 17 de julio de 2015
Démontrer que le triangle ABM est rectangle
Exercice
(C) est un cercle de 2.5 cm de rayon. Le segment [AB] est un diamètre de ce cercle. M est un point de ce cercle tel que AM = 3 cm.
1) Construire la figure.
2) Démontrer que le triangle ABM est rectangle.
3) Calculer la longueur MB.
Déterminer la mesure de l’angle ∠CBA au degré près
Exercice
ABC est un triangle rectangle en A tel que
AB = 7 cm et BC = 12 cm.
1) Faire une figure à main levée.
2) Calculer AC. On donnera la valeur exacte.
3) Déterminer la mesure de l’angle ∠CBA au degré près.
Montrer que N est le milieu de [BC]
Exercice
On considère un triangle ABC tel que AB = 60 mm, BG = 75 mm et CA = 45 mm.
1) Construire le triangle ABC.
2) Montrer que le triangle ABC est rectangle et préciser en quel point.
3) Construire le point M milieu de [AB] et construire la droite parallèle à [AC] passant par M ; elle coupe [BC] en N.
4) Montrer que N est le milieu de [BC].
1) Construire le triangle ABC.
2) Montrer que le triangle ABC est rectangle et préciser en quel point.
3) Construire le point M milieu de [AB] et construire la droite parallèle à [AC] passant par M ; elle coupe [BC] en N.
4) Montrer que N est le milieu de [BC].
Sachant que DC = 5 cm, calculer AB
Exercice
On donne:
Deux droites parallèles (AB) et (CD) , à l'intérieur desquelles deux droites (AC) et (BD) sécantes au point O.
1) Tracer une figure (avec les quatres droites selon les mesures suivantes:
OA = 7.5cm ; OB = 4 cm ;
OC = 3 cm ; et OD = 1.6 cm.
2) Montrer que les droites (DC) et (AB) sont parallèles.
3) Sachant que DC = 5 cm, calculer AB.
Montrer que le triangle ABC est rectangle et préciser en quel point
Exercice
On considère un triangle ABC tel que AB = 6 cm, BC = 7.5 cm et AC = 4.5 cm.
1) Construire le triangle ABC.
2) Montrer que le triangle ABC est rectangle et préciser en quel point.
3) Construire le point M milieu de [AB] et construire la droite parallèle à [AC] passant par M ; elle coupe [BC] en N.
4) Montrer que N est le milieu de [BC].
Quelle est la valeur de tan (∠BAC) ?
Exercice
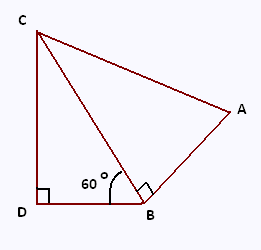
On donne:
BD = 4 cm ; BA = 6 cm et mes(∠DBC) = 60o.
On ne demande pas de faire une figure en vraie grandeur.
1) Montrer que BC = 8 cm.
2) Calculer CD.
Donner la valeur arrondie au dixième.
3) Calculer AC.
4) Quelle est la valeur de tan (∠BAC) ?
5) En déduire la valeur arrondie au degré de ∠BAC.
Calculer l’aire du triangle AMN
Exercice 10
L’unité de longueur est le centimètre.
ABC est un triangle tel que AB = 9 ; AC = 15 ; BC = 12.
1) a) Démontrer que ABC est rectangle en B.
b) Tracer en vraie grandeur le triangle ABC.
2) M est le point du segment [AB] tel que AM = 3.
N est le point du segment [AC] tel que AN = 5.
a) Placer les points M et N sur la figure.
b) Démontrer que la droite (MN) est parallèle à la droite (BC).
3) Calculer l’aire du triangle AMN.
Sur la demi-droite [AC), placer le point M tel que AM = 10.8 cm
Exercice
1) Construire un triangle ABC rectangle en A et tel que AC = 6 cm, BC = 7.5 cm.
2) Montrer par le calcul que AB = 4.5 cm.
3) Sur la demi-droite [AC), placer le point M tel que AM = 10.8 cm. Sur la demi-droite [AB), placer le point N tel que AN = 8.1 cm.
a) Montrer que les droites (BC) et (MN) sont parallèles.
b) Calculer MN.
Calculer la longueur AM
Exercice
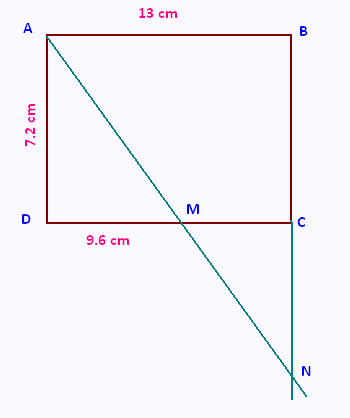
Sur la figure ci-contre, qui n’est pas en vraie grandeur, le quadrilatère ABCD est un rectangle avec AB = 13 cm et AD = 7.2 cm.
Le point M est sur le segment [DC] tel que DM = 9.6 cm. N est le point d’intersection des droites (AM) et (BC).
1) Démontrer que la longueur MC est égale à 3.4 cm.
2) Calculer la longueur AM.
3) Calculer la longueur CN.
En utilisant le théorème de Thalès, calculer AD
Exercice
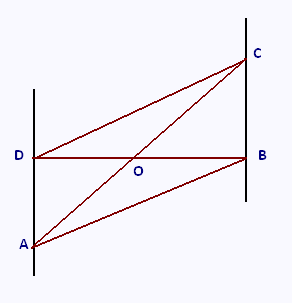
Les points D, O, B d’une part et les points A, O, C d’autre part sont alignés dans cet ordre.
OC = 6 cm : OA = 9 cm ; OD = 5.4 cm et OB = 3.6 cm.
1) Les droites (AD) et (BC) sont-elles parallèles ? Justifier.
2) On suppose que BC = 4.8 cm. Le triangle OBC est-il rectangle ? Justifier.
3) En utilisant le théorème de Thalès, calculer AD.
4) On admettra que les droites (AD) et (DB) sont perpendiculaires. Quelle est l’aire du quadrilatère ABCD ? Justifier.
Faire une figure à main levée
Exercice
ABC est un triangle rectangle en B tel que AB = 8 cm
et l'angle ∠ACB mesure 40o.
1) Faire une figure à main levée.
2) Calculer AC On arrondira la valeur au mm près.
Préciser la nature du triangle AED.
Exercice
Soit ABC un triangle tel que :
AB = 10.4 cm ; AC = 9.6 cm ; BC = 4 cm.
1) Faire une figure qui sera complétée au fur et à mesure.
2) Démontrer que le triangle ABC est un triangle rectangle.
3) Soit D le point du segment [AB] tel que AD = 7.8 cm.
Le cercle (C ) de diamètre [AD] recoupe le segment [AC] en E.
Préciser la nature du triangle AED.
Démontrer que les droites (BC) et (DE) sont parallèles.
4) Calculer DE.
Quelle est la nature du quadrilatère AMBN ?
Exercice
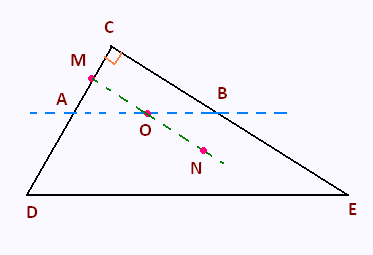
• CDE est un triangle rectangle en C.
• A appartient au segment [CD], B appartient au segment [CE] et la droite (AB) est parallèle à la droite (DE).
• Le point M est le milieu du segment [AC] et le point O est le milieu de [AB].
• Le point N est le symétrique de M par rapport à O.
• DE = 12 cm ; AB = 4.5 cm et AC = 1.8 cm.
1) Quelle est la nature du quadrilatère AMBN ?
2) Montrer que la droite (MO) est parallèle à la droite (CB).
3) Calculer la longueur CD.
4) Calculer une valeur approchée au degré près de l’angle BAC.
Démontrer que AB = 2
Exercice
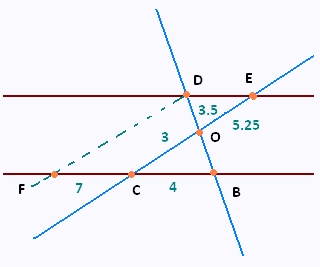
la figure n'est pas à l'échelle.
– les points F, C et B sont alignés dans cet ordre ;
– les segments [CE] et [BD] se coupent au point O;
– les droites (BC) et (DE) sont parallèles.
On donne les longueurs :
BC = 4 ; CO = 3 ; OD = 3.5 ;
FC = 7 ; OE = 5.25.
1) Démontrer que AB = 2.
2) Démontrer que les droites (OC) et (DF) sont parallèles.
Sachant que AP = 2.6 cm et AR = 1.2 cm, montrer que les droites (PR) et (BC) sont parallèles
Exercice
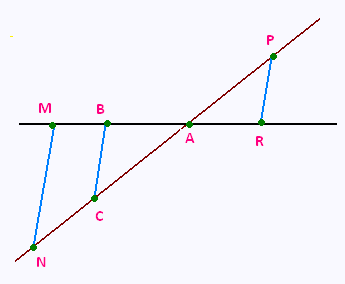
On précisera pour chacune des deux questions de cet exercice la propriété utilisée.
La figure ci-contre n’est pas représentée en vraie grandeur. Les droites (BC) et (MN) sont parallèles.
On donne :
AB = 2.4 cm ; AC = 5.2 cm ;
AN = 7.8 cm et MN = 4.5 cm.
1) Calculer les longueurs AM et BC.
2) Sachant que AP = 2.6 cm et AR = 1.2 cm, montrer que les droites (PR) et (BC) sont parallèles
Calculer la mesure de l’angle ∠ CDA
Exercice
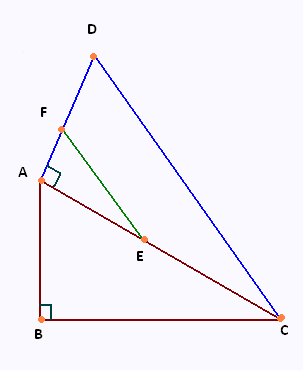
Sur la figure ci-contre:
• Les angles ∠DAC et ∠ABC sont droits,
• L'angle ∠CAB mesure 50o,
• AD = 5 cm, et AC = 7 cm.
1) Calculer BC, puis en donner la valeur arrondie au mm près.
2) Calculer DC. On donnera sa valeur exacte.
3) Calculer la mesure de l’angle ∠ CDA en donnant sa valeur arrondie à un degré près.
4) Les droites (EF) et (CD) sont parallèles et AE = 2.5 cm.
Calculer AF.
On donnera la valeur exacte puis la valeur arrondie au mm près.
Conjecturer la nature précise du quadrilatère ABCD
Exercice
ABCD est un parallélogramme de centre O, tel que AC = 12 cm, BD = 6.4 cm et AB = 6.8 cm.
1) Faire une figure à main levée.
2) Construire ABCD en vraie grandeur.
3) Conjecturer la nature précise du quadrilatère ABCD.
4) Prouver que le résultat observé à la question 3 est vrai
Calculer la hauteur de l’arbre
Exercice
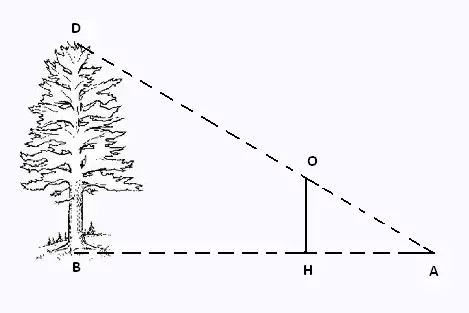
On veut trouver la hauteur BD d’un arbre.
On dispose des renseignements suivants :
HA = 1m ; BH = 5 m et OH = 0.9 m.
Les points A, H et B sont alignés, ainsi que les points O, A et D.
Les angles ∠OHA et ∠DBA sont droits.
1) Démontrer que les droites (OH) et (BD) sont parallèles.
2) Calculer la hauteur de l’arbre.
Démontrer que les angles ∠ABC et ∠AMP sont égaux
Exercice
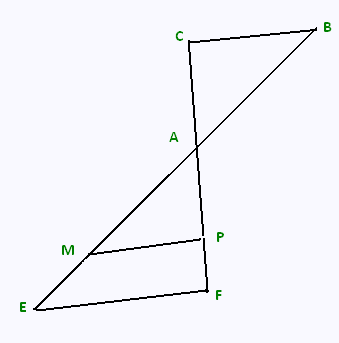
L’unité est le millimètre. La figure ci-contre n’est pas à l’échelle.
On ne demande pas de refaire cette figure.
Les points E, M, A, B sont alignés dans cet ordre.
Les points F, P, A, C sont alignés dans cet ordre.
Les droites (EF) et (MP) sont parallèles.
AM = 60 ; MP = 48 ; AP = 36 ;
EF = 60 ; AC = 45 ; AB = 75.
1) Démontrer que le triangle AMP est un triangle rectangle.
2) Calculer AE et en déduire la longueur ME . Justifier les calculs.
3) Démontrer que les droites (MP) et (BC) sont parallèles.
4) Démontrer que les angles ∠ABC et ∠AMP sont égaux.
Calculer AD
Exercice
La figure suivante n’est pas réalisée en vraie grandeur.
L’unité de longueur est le centimètre.
On donne AB = 8 ; BC = 9 ; AC = 6 ; AE = 4.
1) Les droites (DE) et (BC) sont parallèles.
Calculer AD. On donnera sa valeur exacte puis sa valeur arrondie au dixième de centimètre.
2) Soit F le point tel que C, B et F sont alignés dans cet ordre, avec BF = 6.
3) Démonter que les droites (EF) et (AB) sont parallèles.
Calculer le cosinus de l’angle Â
Exercice
l’unité de longueur est le centimètre.
ABC est un triangle rectangle en C.
D est un point du segment [AB].
E est un point du segment [AC].
On donne :
AC = 6 ; BC = 4.5 ; AD = 4 ;
(DE) // (BC).
1) Faire une figure à main levée.
2) Prouver que AB = 7.5.
3) Calculer AE.
4) a) Calculer le cosinus de l’angle
b) En déduire la mesure, arrondie au degré, de l’angle A.
Montrer que ED = 13
Exercice
On considère deux droites (ED) et (AB), à l'intérieur desquellles les droites (EB) et (DA) sont sécantes en C.
On donne :
CE = 5 , CD = 12 , CA = 18 ,
CB = 7.5 , AB = 19.5.
1) Faire une figure à main levée.
2) Montrer que les droites (ED) et (AB) sont parallèles.
3) Montrer que ED = 13.
4) Montrer que le triangle CED est un triangle rectangle.
5) Calculer tan(∠DEC) puis en déduire la valeur arrondie au degré de la mesure de l’angle ∠DEC
Calculer la distance MN
Exercice
L’unité de longueur est le centimètre.
ABC est un triangle tel que
AB = 6.4 ; BC = 8 et AC = 4.8.
1) Construire la figure en vraie grandeur.
2) Démontrer que le triangle ABC est rectangle en A.
3) Calculer la valeur arrondie au degré près de la mesure de l’angle ∠ABC.
4) M est le point du segment [AB] tel que BM = 4 et N est le point du segment [BC] tel que BN = 5.
a) Démontrer que les droites (MN) et (AC) sont parallèles.
b) Calculer la distance MN.
Prouver que le triangle DIC est un triangle rectangle
Exercice
L’unité de longueur étant le millimètre.
Sient deux segments [AC] et [AB] se coupant en I.
On a :
IB = 21, ID = 27, IA = 28, IC = 36, DC = 45.
1) Faire une figure à main levée
2) Prouver que les droites (AB et (DC) sont parallèles.
3) Calculer la longueur AB.
4) Prouver que le triangle DIC est un triangle rectangle.
5) Déterminer, à un degré près, la mesure de l’angle DCI.
6) Montrer que les angles IDC et IBA ont la même mesure.
Faire la figure en vraie grandeur et calculer AC
Exercice
Soit ABC un triangle rectangle en A tel que :
AB = 6 cm et mes(∠ABC) = 40o.
1) Faire la figure en vraie grandeur.
2) Calculer AC (on donnera la valeur arrondie au mm).
3) Tracer la hauteur issue de A : elle coupe [BC] en H.
Calculer AH et en donner une valeur arrondie au mm.
Deux droites (AC) et (BD) se coupant en E
Exercice
On considère deux droites (AC) et (BD)
se coupant en E.
L’unité de longueur est le millimètre.
On donne :
BC = 70 ; BE = 60 ; EA = 16 ;
ED = 24 ; EC = 40.
1) Faire une figure à main levée.
2) Montrer que les droites (AD) et (BC) sont parallèles.
3) Calculer la longueur AD.
Calculer AD ; en déduire F
Exercice
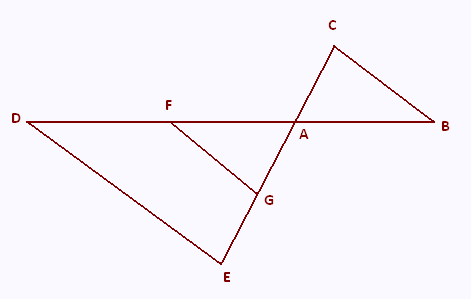
L’unité de longueur est le centimètre.
La figure ci-contre n’est pas à l’échelle.
Les points D, F, A et B sont alignés.
Les points E, G, A et C sont alignés.
Les droites (DE) et (FG) sont parallèles.
AF = 5 ; FG = 3 ; AG = 4 ; DE = 7.5 ;
AC = 3 ; AB = 3.75.
1) Démontrer que le triangle AFG est un triangle rectangle.
2) a) Calculer AD ; en déduire FD.
b) Calculer AE ; en déduire EG.
3) Démontrer que les droites (FG) et (BC) sont parallèles.
Calculer la valeur exacte de la tangente de l’angle ∠CID
Exercice
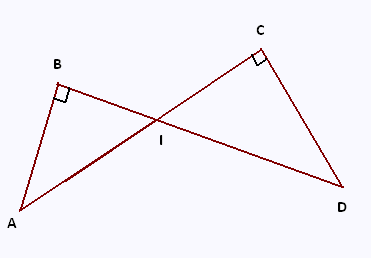
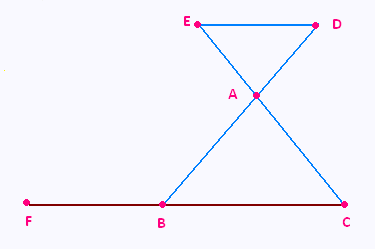
Les segments [AC] et [BD] se coupent au point I.
IC = 4 cm ; CD = 2.4 cm et AB = 4.2 cm.
Le triangle ICD est rectangle en C.
Le triangle AIB est rectangle en B.
1) Calculer la valeur exacte de la tangente de l’angle ∠CID.
2) Pourquoi les angles ∠CID et ∠AIB sont-ils égaux ?
3) Donner l’expression de la tangente de l’angle ∠AIB en fonction de IB.
4) En s’aidant des réponses aux questions précédentes, prouver que la longueur IB en centimètres est un nombre entier.
5) Déterminer l’arrondi au degré de l’angle ∠CID.
Démontrer que les droites (EF) et (DC) sont parallèles
Exercice
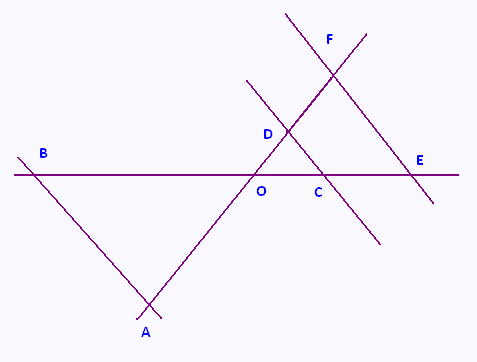
L’unité est le cm. Sur la figure ci-contre, les longueurs ne sont pas respectées. On ne demande pas de reproduire la figure.
On sait que les points B, O, C et E sont alignés dans cet ordre et que les points A, O, D, et F sont alignés dans cet ordre.
On sait également que : (AB // (DC) ; OD = 3 ; OC = 5 ; OA = 5 et DC = 4.
1) Calculer AB en justifiant ; donner la valeur exacte, puis l’arrondir au mm.
2) On sait de plus que : OF = 4.5 et OE = 7.5.
Démontrer que les droites (EF) et (DC) sont parallèles.
Déterminer la mesure de l'angle AMB et justifier
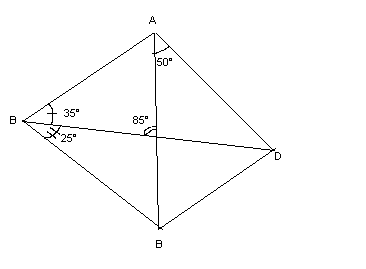
Déterminer la mesure de l'angle AMB et justifier.
Tel que : AMBO est un quadrilatère, AM=MB, AOB = 86°, OAM est rectangle ( =90° ) et MBO aussi !
Tel que : AMBO est un quadrilatère, AM=MB, AOB = 86°, OAM est rectangle ( =90° ) et MBO aussi !
Mesure d’un angle
Exercice :
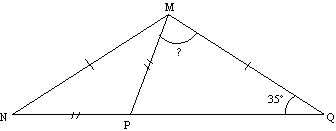
Le triangle MNQ est isocèle de sommet principal M et de base [NQ].
Le triangle PMN est isocèle de sommet principal P et de base [MN].
L’angle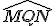 
mesure 
.
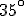Déterminer la mesure de l’angle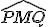 
.
jueves, 16 de julio de 2015
Proporcionalidad
Sur la figure ci-contre, trouver la valeur de x pour que le triangle MOT soit rectangle en M.
Exercices de géométrie I
Exercice 1
Sélectionne
le nom d'un point qui appartient à la droite (CD) mais qui n'appartient pas au
segment [OD].
Seul le point C convient.Matemática, espíritu y arte: Exercices sur le théorème de Thalès III
Matemática, espíritu y arte: Exercices sur le théorème de Thalès III: Exercice 3 Marie souhaite connaître la hauteur d'un arbre. Après quelques mesures elle obtient la figure suivante: Quelle est la...
Exercices sur le théorème de Thalès III
Exercice 3
Marie souhaite connaître la hauteur d'un arbre.
Après quelques mesures elle obtient la figure suivante:
mètres
Marie souhaite connaître la hauteur d'un arbre.
Après quelques mesures elle obtient la figure suivante:
Quelle est la hauteur de l'arbre, arrondie à 0,1 mètre près?
Exercices sur le théorème de Thalès II
Exercice 2
A quoi sert la réciproque du théorème de Thalès?
A calculer des
longueurs
A démontrer que des droites sont perpendiculaires
A démontrer que des droites sont parallèles
A calculer des angles
A démontrer que des droites sont perpendiculaires
A démontrer que des droites sont parallèles
A calculer des angles
Exercices sur le théorème de Thalès I
Exercices sur le théorème
de Thalès
Exercice
1
A quoi sert le théorème de Thalès?
A quoi sert le théorème de Thalès?
A démontrer (prouver) que
des droites sont parallèles
A démontrer (prouver) que des droites ne sont pas paralleles
A calculer des angles
A calculer des longueurs
A démontrer (prouver) que des droites ne sont pas paralleles
A calculer des angles
A calculer des longueurs
Il sert effectivement
à calculer des longueurs.
miércoles, 15 de julio de 2015
martes, 14 de julio de 2015
lunes, 13 de julio de 2015
domingo, 12 de julio de 2015
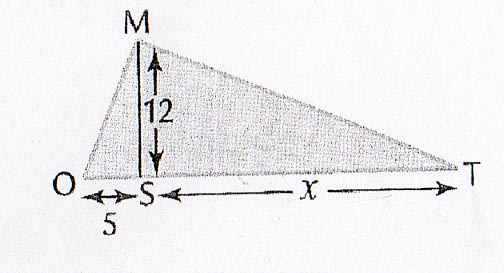
Triángulos en el Plano: What is the area x of the triangle ABD? - Quelle ...
Triángulos en el Plano: What is the area x of the triangle ABD? - Quelle ...: Dans le croquis ci-dessous, on donne les mesures des côtés AB et BC ainsi que l’aire du triangle BCD. Quelle est l’aire x du triangle ABD? ...
sábado, 11 de julio de 2015
sábado, 4 de julio de 2015
viernes, 3 de julio de 2015
Números Naturales: Evaluation - Évaluation - Prova di valutazione
Números Naturales: Evaluation - Évaluation - Prova di valutazione: Evaluación v Divisores de 16 v Divisores de 20 v Divisores de 28 v M.C.D. (16, 20, 28) v Con una tabla de doble entrada ...
jueves, 2 de julio de 2015
miércoles, 1 de julio de 2015
Suscribirse a:
Entradas (Atom)