Ley de Ohm III

Ohm's Law,
Example Three
Given the resistor arrangement shown below, prove that the relation between R₁ and R₂ must be R₂=1.618R1 in order that the resistance of the system R be equal to R₂.

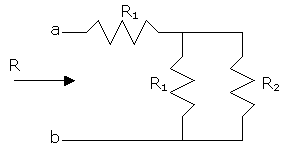
R=R₁+R₁//R₂=R₁+R₁R₂/(R₁+R₂).
The condition is R=R₂, so we do
R₂=R₁+R₁R₂/(R₁+R₂).
R₁R₂+R₂²=R₁²+R₁R₂+R₁R₂.
0= R₂² - R₁R₂ - R₁².

This is a second degree equation in R₂, whose solution is R₂= R₁(1/2 ± )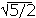

Disregarding the minus sign we get R₂ = 1.618R₁