miércoles, 30 de septiembre de 2015
domingo, 20 de septiembre de 2015
Clasificación de triángulos
Consider each of the triangles below. Circle all that apply to the triangle.
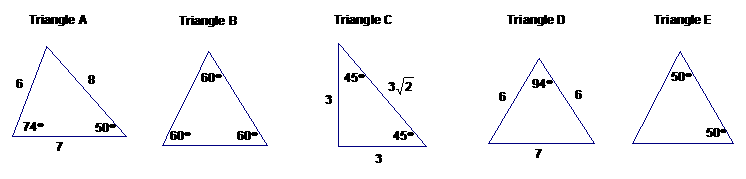
1. Acute Obtuse Right Scalene Isosceles Equilateral
2. Acute Obtuse Right Scalene Isosceles Equilateral
3. Acute Obtuse Right Scalene Isosceles Equilateral
4. Acute Obtuse Right Scalene Isosceles Equilateral
5. Acute Obtuse Right Scalene Isosceles Equilateral
domingo, 13 de septiembre de 2015
sábado, 12 de septiembre de 2015
viernes, 11 de septiembre de 2015
miércoles, 9 de septiembre de 2015
Trabajo I
Let's see an exercise.
A 40 kg box is dragged 30 m on a horizontal floor, applying a Fp = 100 N exerted by a person. Such force acts doing a 60º angle. The floor exerts a friction force Fr = 20 N. Calculate the work done for each one of these forces Fp, Fr, the weight mg and the normal. Calculate also the net work done on the box.
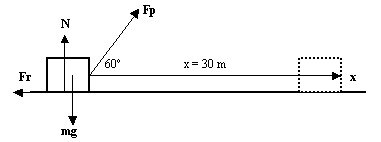
The work done by mg and the normal N is zero, because they are perpendicular to displacement(
The work done by Fp is:
Wp = Fpxcos
The work done by the friction force Fr is:
Wr = Frxcos180º = (20 N)(30 m)(-1) = -600 J.
The angle between Fr and displacement is 180º because they point in opposite directions.
The net work can be calculated in two equivalents ways:
- As the algebraic sum of the work done by each force:
WNET = 1500 J +(- 600 J) = 900 J. - Finding first the net force on the object along the displacement:
F(NET)x= Fpcos - Fr
- Fr
and then doing
WNET = F(NET)x = (Fpcos - Fr)x= (100 Ncos60º - 20 N)(30 m) = 900 J.
- Fr)x= (100 Ncos60º - 20 N)(30 m) = 900 J.
Ley de Ohm III
Ohm's Law,
Example Three
Given the resistor arrangement shown below, prove that the relation between R1 and R2 must be R2=1.618R1 in order that the resistance of the system R be equal to R2.
Example Three
Given the resistor arrangement shown below, prove that the relation between R1 and R2 must be R2=1.618R1 in order that the resistance of the system R be equal to R2.
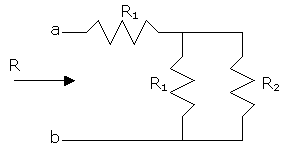
R=R1+R1//R2=R1+R1R2/(R1+R2).
The condition is R=R2, so we do
R2=R1+R1R2/(R1+R2).
R1R2+R22=R12+R1R2+R1R2.
0= R22 - R1R2 - R12.
The condition is R=R2, so we do
R2=R1+R1R2/(R1+R2).
R1R2+R22=R12+R1R2+R1R2.
0= R22 - R1R2 - R12.
This is a second degree equation in R2, whose solution is R2= R1(1/2 ± 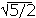 )
)
Disregarding the minus sign we get R2 = 1.618R1
Ley de Ohm II
Ohm's Law,
Example Two
Determine the total resistance and potential difference between points a and b in the circuit shown. Also determine the current in, and the potential difference across, each resistor. The input current is 60 A.
Example Two
Determine the total resistance and potential difference between points a and b in the circuit shown. Also determine the current in, and the potential difference across, each resistor. The input current is 60 A.
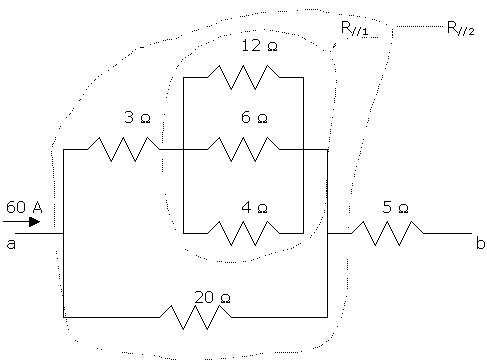
a) Total resistance between a and b.
First, calculate the 12, 6, and 4 ohm parallel combination R//1
 1/R//1 = 1/12 + 1/6 + 1/4 = 1/2. Then R//1 = 2 ohm.
1/R//1 = 1/12 + 1/6 + 1/4 = 1/2. Then R//1 = 2 ohm.
The upper branch is 3 ohms in series with R//1, 3 ohm + 2 ohm = 5 ohm.
This 5 ohm resistor is in parallel with the 20 ohm resistor, equivalent to a single resistor R//2 = 5 ohm//20 ohm:
 1/R//2 = 1/5 + 1/20 = ¼. Then R//2 = 4.
1/R//2 = 1/5 + 1/20 = ¼. Then R//2 = 4.
The total resistance between a and b is 4 ohm + 5 ohm = 9 ohms. The voltage drop or potential difference between points a and b is 60Ax9ohm = 540 V.
The total resistance between a and b is 4 ohm + 5 ohm = 9 ohms. The voltage drop or potential difference between points a and b is 60Ax9ohm = 540 V.
b) To obtain the individual currents and voltages in each resistor we can proceed as follows (there is no a unique method):
The voltage across R//2 is the difference between the total 540 voltage and the voltage drop in the 5 ohm resistor. This drop is 60Ax5ohm = 300 V. So the potential difference across R//2 is 540 V – 300 V = 240 V.
Now we can calculate the currents and voltages in the R//2combination:
In the 20 ohm resistor: current= 240 V/20 ohm = 12 A, voltage = 240 V
The upper branch has then a current of 60 A - 12 A = 48 A, or alternatively 240 V/5 ohm = 48A.
The 3 ohm resistor has a voltage of 48 Ax3 ohm = 144 V.
The R//1 combination presents a voltage of 48 AxR//1 = 48 Ax2 ohm = 96 V, or alternatively 240 V - 144 V = 96 V.
The currents in the 12 ohm, 6 ohm and 4 ohm are respectively 96/12 A=8 A, 96/6=16 A and 96/4=24 A
Now we can calculate the currents and voltages in the R//2combination:
In the 20 ohm resistor: current= 240 V/20 ohm = 12 A, voltage = 240 V
The upper branch has then a current of 60 A - 12 A = 48 A, or alternatively 240 V/5 ohm = 48A.
The 3 ohm resistor has a voltage of 48 Ax3 ohm = 144 V.
The R//1 combination presents a voltage of 48 AxR//1 = 48 Ax2 ohm = 96 V, or alternatively 240 V - 144 V = 96 V.
The currents in the 12 ohm, 6 ohm and 4 ohm are respectively 96/12 A=8 A, 96/6=16 A and 96/4=24 A
Ley de Ohm I
Ohm's Law,
Example One
The circuit below is called a Wheatstone bridge. It is used for measuring resistance. Show that when the current through the galvanometer G is zero, then R1 = R2(R3/R4). Thus, if we know R2 and the ratio (R3/R4), we can obtain the resistance R1.
Example One
The circuit below is called a Wheatstone bridge. It is used for measuring resistance. Show that when the current through the galvanometer G is zero, then R1 = R2(R3/R4). Thus, if we know R2 and the ratio (R3/R4), we can obtain the resistance R1.
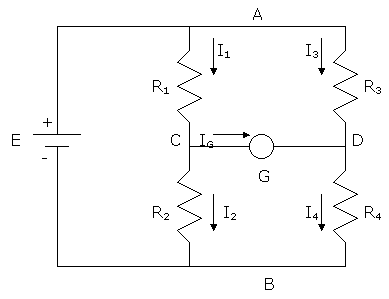
IG = 0 means points C and D are at the same potential and
that I1 = I2, I3 = I4.
that I1 = I2, I3 = I4.
By Ohm’s law VAC = I1R1, VAD = I3R3, VCB = I2R2, VDB = I4R4.
As VAC = VAD and VCB = VDB, then I1R1= I3R3,
 I2R2= I4R4.
I2R2= I4R4.
As I1 = I2 and I3 = I4, then doing I1R1/ I2R2=I3R3/I4R4 we get R1= R2(R3/R4)
martes, 8 de septiembre de 2015
domingo, 6 de septiembre de 2015
Ángulos
Responder SIEMPRE, AVECES
O NUNCA :
a) Dos ángulos
adyacentes son consecutivos
b) Dos ángulos adyacentes son suplementarios
c) Los ángulos opuestos por el vértice son complementarios
d) El complemento de un ángulo agudo es un ángulo obtuso
e) Dos ángulos consecutivos son complementarios
f) El complemento de un ángulo recto es un ángulo nulo
g) Dos ángulos opuestos por el vértice son suplementarios
b) Dos ángulos adyacentes son suplementarios
c) Los ángulos opuestos por el vértice son complementarios
d) El complemento de un ángulo agudo es un ángulo obtuso
e) Dos ángulos consecutivos son complementarios
f) El complemento de un ángulo recto es un ángulo nulo
g) Dos ángulos opuestos por el vértice son suplementarios
sábado, 5 de septiembre de 2015
jueves, 3 de septiembre de 2015
miércoles, 2 de septiembre de 2015
martes, 1 de septiembre de 2015
Suscribirse a:
Comentarios (Atom)