miércoles, 29 de abril de 2015

Números Racionales: Multiplicación y División de Racionales

domingo, 26 de abril de 2015

Teorema de Pitágoras: teorema de Pitágoras

Teorema de Thales: Teorema de Thales

Matemática, espíritu y arte: Teorema de Thales

Matemática - Propiedades: Teorema de Thales

Matemática - Propiedades: Segmentos Proporcionales

Matemática - Propiedades: Matemática - Propiedades

Números Naturales: Función y Gráfico - Function and Graph

M014---DIVISIÓN(3) Por UNA CIFRA

Inecuaciones - Inequalities: Inecuaciones - Inequalities

sábado, 25 de abril de 2015

Programa de Matemática de Primer Año

PROGRAMA DE 1er Año – MATEMÁTICA

UNIDAD 1: Números

♦ Unidad, decena y centena de mil de millón.

♦ Uso de los números naturales

♦ Relaciones de menor y mayor que, igual, anterior, siguiente, más o menos que

♦ Escalas

♦ Escrituras equivalentes de un número

♦ Sistemas de numeración no posicional y posicional: romano, decimal.

Propiedades.

♦ Reglas de escritura y lectura.

♦ Fracciones positivas: concepto, usos, clasificación formas de representación,

comparación,

♦ Equivalencias, simplificación, amplificación, expresiones decimales.

♦ Decimales positivos: concepto, usos, comparación, orden, formas de representación,

recta numérica.

♦ Equivalencias entre formas de escritura decimal y fraccionaria.

UNIDAD 2: Operaciones

♦ Números naturales: suma y resta, multiplicación de números de más de tres

cifras.

♦ Unidad de seguida de ceros. División: números de más de tres cifras.

♦ La unidad seguida de ceros.

♦ Potencias y raíces exactas de números inferiores a cien. Algoritmos de cada

operación.

♦ Uso de propiedades: conmutativa, asociativa y distributiva.

♦ Ecuaciones simples.

♦ Divisibilidad. Números primos y compuestos.

♦ Descomposición en factores primos. M.C.M. y D. M. C. Problemas de conteo.

♦ Números fraccionarios: suma y resta de distinto denominador. Equivalencias.

♦ Números decimales: suma, resta, multiplicación. Multiplicación entero por

decimal, decimal por decimal. División. Ecuaciones.

♦ Cálculo exacto y aproximado con los distintos tipos de números en forma

mental, escrita y con calculadora. Estrategias de aproximación.

♦ Proporcionalidad directa e inversa.

♦ Porcentaje. Funciones de variables directa e inversamente proporcionales.

Gráfico, repartición proporcional

♦ Combinación de operaciones: con paréntesis, con separación en términos.

UNIDAD 3: Nociones geométricas

♦ Sistema de referencia para la ubicación de puntos en una línea y plano.

♦ Punto recta y plano. Representación semirrecta, segmento, comparación y

medición de segmentos.

♦ Segmentos consecutivos y no consecutivos.

♦ Rectas paralelas y secantes (oblicuas y perpendiculares). Distancia entre dos

puntos

♦ Ángulos cóncavos y convexos.: concepto, clasificación, construcción. Relaciones entre ángulos.

♦ Bisectriz.

♦ Polígonos: elementos, clasificación de acuerdo con sus propiedades.

♦ Triángulo: clasificación (según sus lados y sus ángulos). Construcción. Triángulos rectángulos: relación entre hipotenusa y catetos.

♦ Cuadriláteros: clasificación, construcción.

♦ Polígonos de más de cuatro lados. Clasificación, construcción.

♦ Circunferencia y Círculo: reconocimiento y construcciones.

♦ Cuerpos: elementos propiedades y construcciones.

UNIDAD 4: Mediciones

♦ Nociones de medida:

♦ Ángulos: medición

♦ Sistema legal argentino (SIMELA): longitud. Unidad, múltiplos y

submúltiplos.

♦ Pasaje de unidades. Capacidad y peso. Unidad, múltiplos y submúltiplos.

Pasaje de unidades. Unidades convencionales. Medidas de superficie.

♦ Tiempo. Unidades, equivalencias. Operaciones.

♦ Sistema sexagesimal. Operaciones.

♦ Perímetro. Concepto. Comparación de perímetro de figuras. Longitud de la

circunferencia.

♦ Área: concepto. Unidades. Equivalencias. Área de los polígonos más comunes.

♦ Equivalencia de figuras.

♦ Cálculo de medidas: estimación, aproximación.

UNIDAD 5

Estadística y Probabilidad

♦ Nociones elementales de estadística

♦ Lectura de gráficos simples.

♦ Recolección de datos.

♦ Construcción de gráficos: barras; polígonos de frecuencia.

Operaciones Matemáticas: Ecuaciones

Operaciones Matemáticas: Decimales

viernes, 24 de abril de 2015

Suma de Fracciones de Distinto Denominador

Multiplicación, Suma y Resta de Racionales

Fractions Number Line - Fracciones en la Recta Numérica

jueves, 23 de abril de 2015

Decimales Racionales e Irracionales

Propiedades de la Potenciación en Q

miércoles, 22 de abril de 2015

martes, 21 de abril de 2015

CLASE 5: VALOR ABSOLUTO DE UN NÚMERO ENTERO.

MCV4U - Second Derivatives - Part 1 of 2

Inecuaciones con Valor Absoluto

Valor Absoluto: Propiedades

En la propiedad 6, el valor de b tiene que ser distinto de 0 (cero) porque la división por cero no está definida.

Propiedades del Valor Absoluto

Propiedades de la Suma y de la Multiplicación en Q

lunes, 20 de abril de 2015

Unidades de Conversión - Unit Conversion

domingo, 19 de abril de 2015

Ecuaciones Simultáneas - Simultaneous Equations

sábado, 18 de abril de 2015

Teorema de Pitágoras: Demostración Empírica

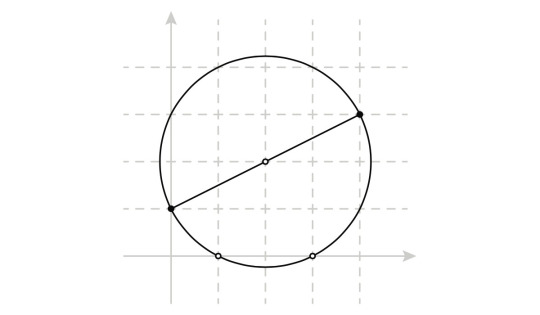
Thomas Carlyle was a Scottish philosopher and teacher, and discovered a geometric interpretation for solving quadratic equations. If you start with the equation x2 – sx + p = 0, and construct the circle with the line joining (0, 1) and (s, p) as a diameter, then the abscissas of the points where the circle intersects the x-axis are exactly the roots of the polynomial.

For instance, consider x2 – 4x + 3 = 0. Its Carlyle circle intersects the x-axis in 1 and 3, which are indeed the solutions of the quadratic equation!

Carlyle circles can be used for developing explicit ruler-and-compass constructions of regular polygons.

Multiplicación Especial

Orden operatorio

División exacta

Números Naturales - Criterios de Divisibilidad

DIVISIBILIDAD – CRITERIOS : Para facilitar la búsqueda de los divisores de un número, es muy importante conocer los Criterios de Divisibilidad, que son reglas que permiten saber si un número es divisible por otro sin necesidad de realizar la división.

Criterios de Divisibilidad correspondientes a los primeros números primos

Número	Regla
2	Un número es divisible por 2 cuando termina en cero o en cifra par. 20, 72, 134, 216, 3218, 58616
3	Un número es divisible por 3 si la suma de sus cifras es múltiplo de 3. (Si la suma es mayor que 9 se suman de nuevo sus cifras). 12 (1+2=3), 132 (1+3+2=6), 261 (2+6+1=9), 753 (7+5+3=15, 1+5=6)
5	Un número es divisible por 5 cuando termina en 0 o en 5. 10, 25, 40, 65, 125, 3215
7	Un número es divisible por 7 cuando la diferencia entre el número, sin la cifra de las unidades, y el doble de la cifra de las unidades es 0 o múltiplo de 7. Si la diferencia es mayor que 77, repetimos el proceso, 84→8 - (2x4) = 8 - 8 = 0 ⇔ 238 →23 - (2x8) = 23 - 16 = 7 2807 →280 - (2x7) = 280 - 14 = 266→26 -(2x6) = 26 - 12 = 14 = 2x7
11	Un número es divisible por 11 si la diferencia entre la suma de las cifras que ocupan lugares pares y la suma de las cifras que ocupan lugares impares es 0, o múltiplo de 11. 132→(2+1 = 3; 3-3 = 0)⇔2816→(8+6 = 14; 2+1 = 3; 14-3 = 11) 71929→ (7+9+9 = 25; 1+2 = 3; 25-3 = 22 = 2x11)

Criterios de Divisibilidad correspondientes a los primeros números compuestos

Número	Regla
4	Un número es divisible por 4 si el número formado por sus dos últimas cifras es múltiplo de 4. 104, 208, 312, 716, 920, 1148, 2172, 35796
6	Un número es divisible por 6 si es divisible por 2 y por 3 al mismo tiempo, es decir termina en cifra par y la suma de sus cifras es múltiplo de 3. 72→(7+2=9), 114→(1+1+4=6), 4368→(4+3+6+8=21, 2+1=3)
8	Un número es divisible por 8 si el número formado por sus tres últimas cifras es múltiplo de 8. 1008, 2016, 3024, 4032, 13040.
9	Un número es divisible por 9 si la suma de sus cifras es múltiplo de 9. (Si la suma es mayor que 9 se suman de nuevo sus cifras). 72→(7+2=9), 261→(2+6+1=9), 684→(6+8+4=18, 1+8=9)
10	Un número es divisible por 10 cuando termina en 0. 30,120, 3320,12460